기사 메일전송

[칼럼] 메시아를 기다리는 PEG 공식

윤진기 경남대 명예교수

기사등록 2022-08-18 17:08:42

[윤진기 경남대 명예교수·전 한국중재학회 회장] 영국의 저명한 투자자인 짐 슬레이터(Jim Slater)가 PEG 공식을 혁신한 후에 PEG 계산의 불명확성이 다소 완화되어, 일반인들도 쉽게 PEG를 계산할 수 있게 되었다. 당시에 짐 슬레이트는 PEG 공식을 “예상 PEG=1년 후 예상 PER/1년 후 예상 EPS증가율”로 제시하였고, 예상 PEG≤0.75이면 투자하기 좋은 기업이라고 하였다.

짐 슬레이트의 PEG 공식과 그가 제시한 판단기준을 토대로 제작한 PEG공식. [이미지=버핏연구소]

그러나 이 공식은 PER이 음수이면 바로 망가져서 사용할 수 없게 되어버린다. 최근에는 HTS 카이로스, 네이버(NAVER)에서 제공하는 재무데이터처럼 음수 PER을 있는 그대로 음수로 표시하는 금융데이터가 늘어나고 있고, 인터넷에도 음수 PER에 대한 글들이 심심찮게 보인다.

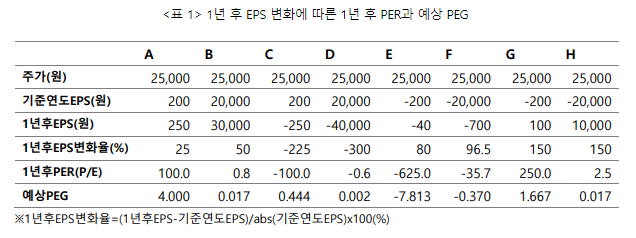
다음 <표 1>은 짐 슬레이트의 PEG 공식 “예상 PEG=1년 후 예상 PER/1년 후 예상 EPS 증가율”을 적용하여 적자기업이 포함된 여러 기업의 1년 후 PER과 예상 PEG를 구한 것이다.

[이미지=버핏연구소]

위 표에서, C, D, E, F는 1년 후 EPS가 적자인 경우이다. 이 경우 EPS가 기준 연도보다 더 감소한 경우에는 C와 D에서 보는 것처럼 변화율이 음수로 나타나고, 기준 연도보다 더 증가한 경우에는 E와 F처럼 양수로 나타난다. 당연한 결과이다. 또한 EPS가 음수이기 때문에 1년 후 PER은 모두 음수로 나타난다.

그런데, 예상 PEG는 C와 D의 경우에는 양수로, E와 F의 경우에는 음수로 나타난다. 이상하게도 C와 D처럼 EPS가 적자 전환하여 변화율이 음수가 된 경우에는 예상 PEG가 양수로 나타나고, 그것도 수치가 0.444와 0.002여서 매수 범위에 드는 매우 좋은 예상PEG를 보여준다. 그러나 이 예상 PEG를 기준으로 C와 D의 주식을 매수한 사람은 거의 망할 것이다. 매수 후에 기업은 계속 적자 폭을 늘여갈 것이기 때문이다.

반면에, E와 F처럼 EPS가 적자이지만 1년 후에는 적자 폭이 대폭 줄어든 경우에 그 변화율은 양수로 나타나고, 1년 후 PER은 1년 후 EPS가 여전히 적자이기 때문에 음수로 나타난다. 그 결과 예상 PEG는 당연히 음수가 된다.

전통 PEG 이론에서는 음수 PEG를 예상하지 않는다. 기본적으로 EPS가 적자여서 PER을 계산하지 않고, (이 경우 실무에서는 데이터를 비워 두고 이빨이 빠졌다고 한다) 이 상태에서는 PEG를 계산할 수 없기 때문이다. 그래서 음수 PER을 인정하고 그대로 사용하여 예상 PEG가 음수로 나오는 경우에는 아마도 그 주식을 매수 고려의 대상에서 제외하게 될 것이다.

그런데, E와 F는 1년 후에 회사가 적자 폭을 대폭적으로 줄일 것으로 예상되고 있어서, 업황이 호전되거나 그동안의 회사의 내부 문제가 해소되어가고 있는 중으로 생각된다. 이런 회사의 주식을 매수 고려 대상에서 제외해버리는 것은 현명하지 않아 보인다. 아이러니하게도 이런 회사의 주식은 종종 대박을 가져온다.

PEG 공식의 계산 결과가 현실에 부합하지 않게 된 이런 현상은 금융데이터에서 음수 PER을 인정하면서부터 야기된 것이지만, PEG 공식의 이러한 문제는 PEG 공식이 본질적으로 가지고 있는 수학적인 한계인 것이다.

그럼에도 불구하고, 세간에는 PEG를 입이 마르도록 칭찬하고, 또 평생 PEG를 이용하여 주식을 매수하여 고객들에게 큰 돈을 벌어준 전설적인 펀드매니저도 있다. 수학적 관점에서는 완전히 엉터리 같은 이 PEG 공식을 제대로 활용하기 위해서는 무엇을 해야 할까? 대체로 다음과 같은 세 가지 대안을 생각해 볼 수 있을 것이다.

첫째, 안되는 것은 포기하고, 원래 PEG 사용자들처럼 양수인 PER의 경우에만 PEG를 계산하는 것이다. PEG에 관한 책을 쓴 짐 슬레이트는 영국 FTSE 올셰어 지수(FTSE All-Share Index) 소속 종목의 50% 이하만 PEG 수치를 부여받고 있다고 한다. 이것만 가지고도 실무에서 PEG 공식을 유용하게 활용할 수 있다.

둘째, PEG 공식의 한계를 받아들이고 PEG를 계산할 때는 항상 실제의 EPS와 변화율을 살펴보고 그때 그때 적절한 해석을 해가며 사용하는 것이다. 그러나 이러한 방법은 PEG값이 양수이든 음수이든 모두 신경을 써서 살펴봐야 하기 때문에 투자자들을 쉽게 지치게 만들 것이다.

셋째, PEG 공식을 새롭게 변혁하여 PER이 음수이든 양수이든 상관없이 투자자들이 편하게 PEG 공식을 사용할 수 있도록 하는 것이다. 그러면 빅데이터에서도 자동으로 PEG값을 계산해 줄 수 있어 재무데이터의 혁신이 일어날 수 있다. 그러나 이 방법은 수학적 계산 결과를 바꾸는 것이라서 엉뚱한 천재가 갑자기 나타나서 해결해 주지 않는 한 쉽지 않아 보인다.

세상일이 그렇듯이, 불가능해 보이는 것들에 대해서는 그것을 해결해 주는 메시아가 그리운 것이다. PEG의 실용성과 간결함에 매료된 마니아들은 아마도 현재 PEG 공식이 직면한 문제를 해결해 주는 메시아를 기다리고 있는지도 모를 일이다.

윤진기 경남대 명예교수(전 한국중재학회 회장). [사진=더밸류뉴스]